[자연어처리] 조건부 확률, 베이즈 정리
*데이터 분석에서 통계, 선형대수학 개념이 많이 활용되기에 학부과정이라면, 잘 숙지해두는 것이 용이하다.
▶ 조건부 확률 : 어떤 사건 A가 일어났다고 가정한 상태에서 사건 B가 일어날 확률
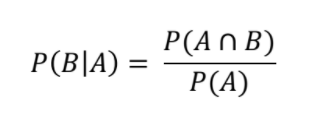
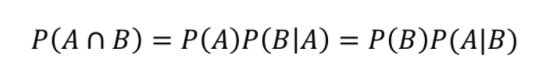
- 전체 표본공간을 다루던 확률을 사건A로 축소해줄 수 있어 이 개념이 많이 활용된다
- 조건부 확률에서 'l' (조건부확률 기본식 예시에서 A)의 의미는 B의 확률을 계산하기 위해서 주어진 문맥, 히스토리, 지식으로 해석할 수 있다
* ex. 주사위를 던져 2가 나올 확률은 1/6, 주사위를 던져 나온 짝수값 중에서 2가 나올 확률은 1/3
- 만약 A와 B가 독립이라면 확률 계산에 영향을 미치지 않는다
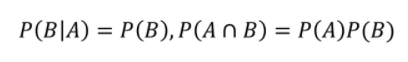
- 지금까지 예시는 두 사건을 가지고 가정을 하는 중이었다. 이는 아래와 같이 확장도 가능하다
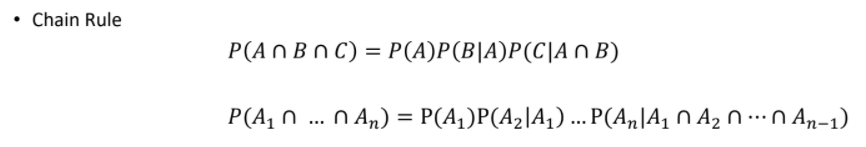
▶ 베이즈 정리 : 두 확률 변수의 사전확률과 사후 확률(조건부 확률) 간의 관계를 나타내는 정리
-어떤 사건이 서로 배반하는 두 원인에 의해 일어났다고 가정하고, 실제 사건이 발생했을 때 이 사건이 두 원인 중 하나일 확률을 구하는 정리, 즉 조건부 확률을 구하는 것을 의미
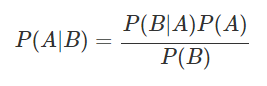
- 사전확률 : P(A), 사건 B가 일어나기 전 가지고 사건 A의 확률
- 사후확률: P(AlB), 사건 B가 발생했다는 문맥에서 사건 A의 확률
- 가능도(likelihood): P(BlA) (향후 MLE, MAP 등에도 자주 활용되기에 개념의 존재를 알아두면 좋다)
→ 베이즈 정리를 활용하면, 사후 확률값을 사전확률값과 P(B), P(BlA)값이 있으면 구할 수 있게 된다
예를 들어, 우리가 양성이 나온 사람 중 실제로 병에 걸린 확률을 구하고 싶다고 가정하자. : P(병ㅣ양성)
그러면 우리는 실제로 병에 걸린 사람의 확률 : P(병) ,
병에 걸린 사람 중 양성이 나온 사람 : P(양성ㅣ병) ,
양성 판정이 나온 사람의 확률 : P(양성)
을 알고 있다면 우리가 구하고자 하는 값을 구할 수 있게 된다.
베이즈 정리는 역확률 문제를 해결하기 위한 방법이다. (역확률이란 확률을 역으로 추적하는 것이라 생각하면 되겠다.)
확률을 추적하기 위해 베이즈 정리를 활용하기 위해선 사전확률: P(병), P(양성)을 알고 있어야 한다.
옛날에는 사회 통계와 같은 전수조사가 어려웠으나, 현재에 빅데이터를 통해 사전확률을 대략적으로 알 수 있게 되어 주로 빅데이터를 다루는 분석에서 많이 활용되는 개념이다.